큐와 토픽
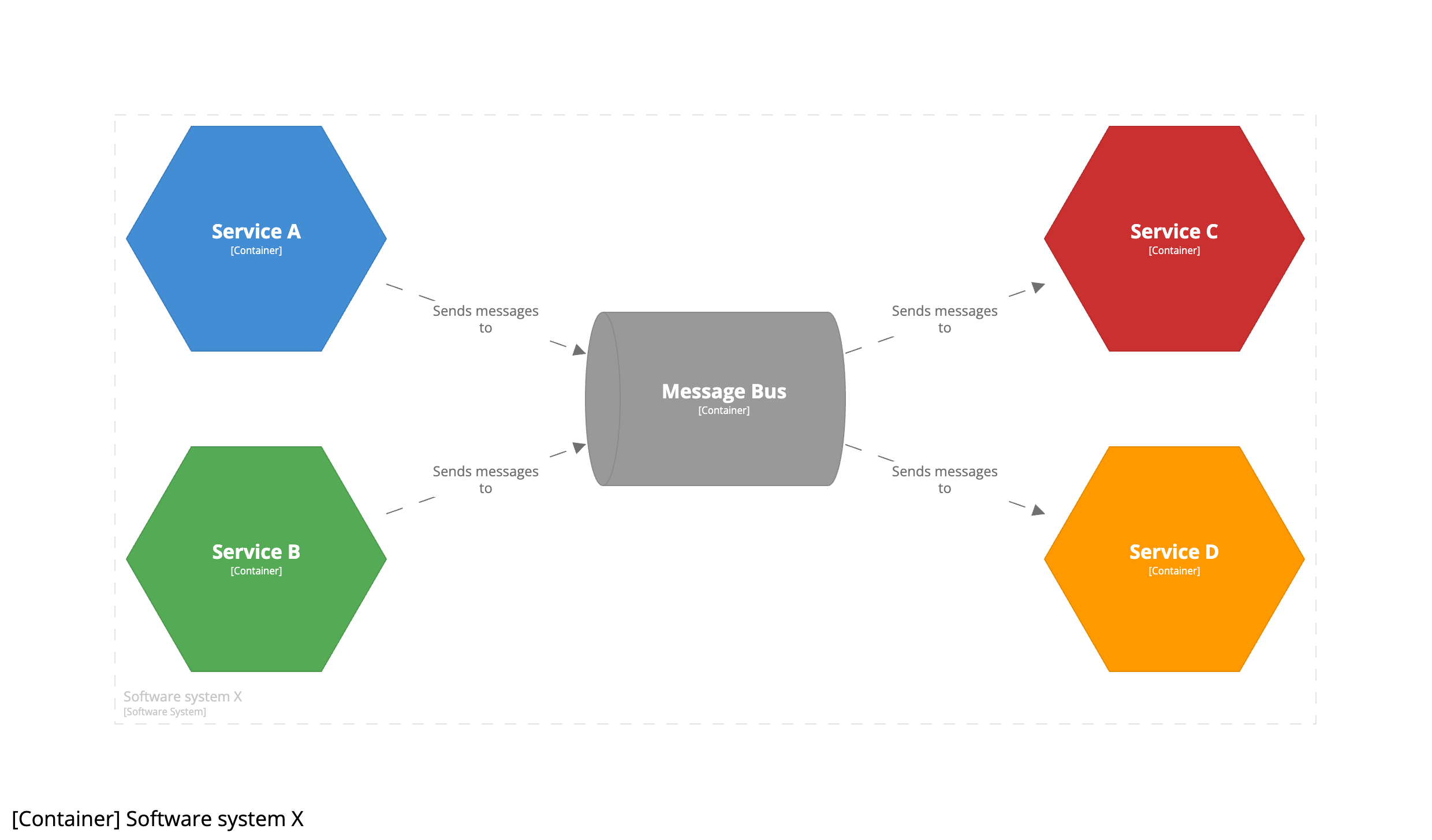
여러 서비스(A와 B)가 메시지를 생성하고 여러 다른 서비스(C와 D)가 메시지를 소비하는 서비스 기반 아키텍처가 있다고 상상해 보세요. 이러한 아키텍처를 다이어그램화하는 일반적인 방법은 다음과 같습니다.
어떤 관점에서 보면 이 다이어그램은 아키텍처를 사실적이고 정확하게 표현한 것입니다. 서비스 A와 B는 중개자에게 메시지를 보내고, 중개자는 해당 메시지를 서비스 C와 D로 전달합니다. 문제는 이 다이어그램의 “허브 앤 스포크” 특성으로 인해 메시지 생산자와 소비자 사이에 어느 정도의 결합이 존재할 수 있는 실제 상황을 모호하게 만드는 경향이 있다는 것입니다.
점대점(Point-to-point)
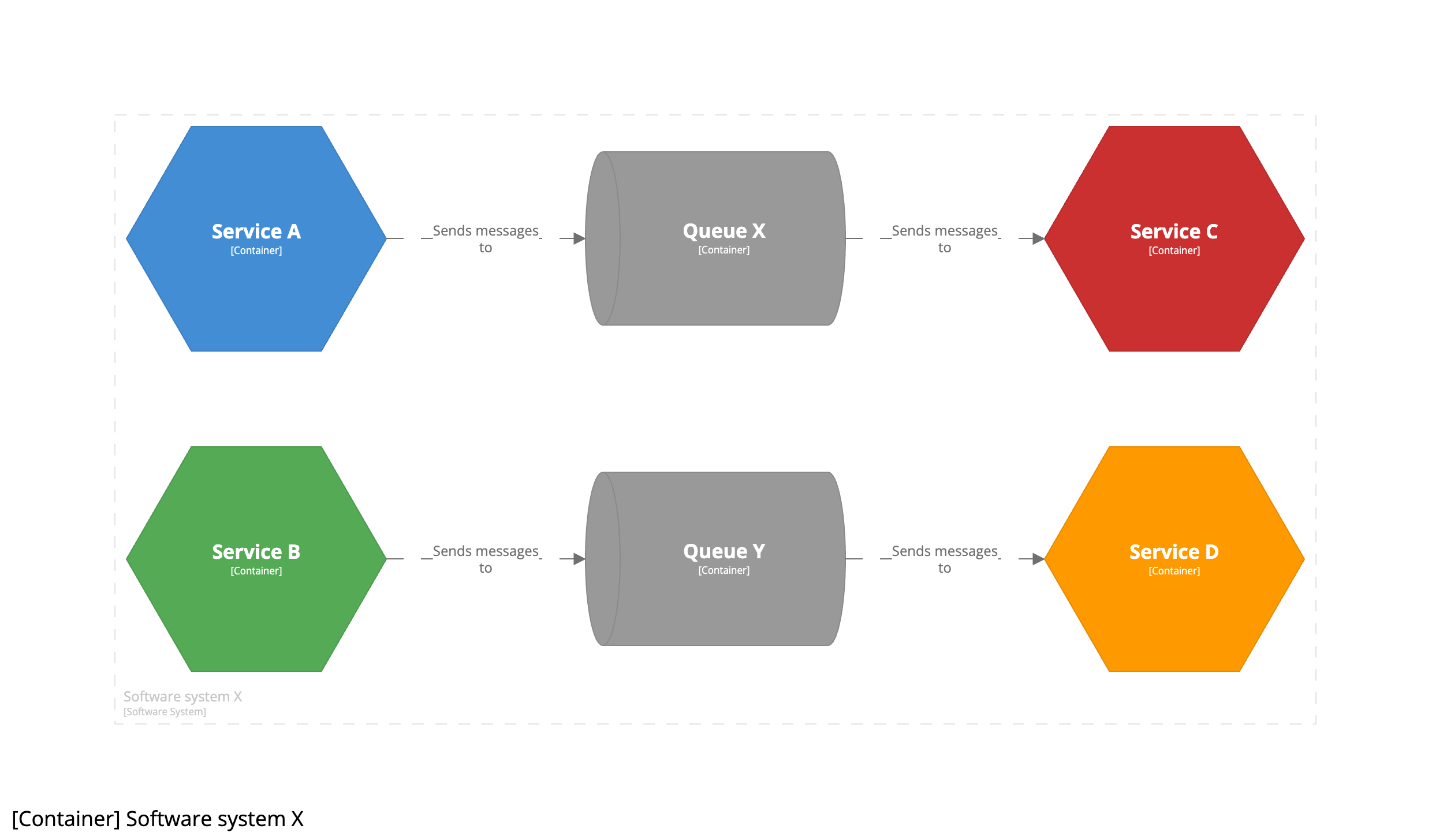
이 문제는 메시지 버스를 C4 컨테이너로 잘못 표현한 데서 비롯됐습니다. 이는 명백히 잘못됐습니다. 더 나은 접근 방식은 각각의 개별 큐와 토픽을 “데이터 저장소”로 생각하는 것입니다. 메시지 큐는 본질적으로 데이터 저장소이며, 생산자가 데이터를 추가하고 소비자가 데이터를 가져가는 데이터(메시지)를 저장하는 버킷입니다. 여기서 중요한 것은 큐와 토픽이 메시지 버스 자체가 아니라 C4 컨테이너라는 점입니다.
이 예제에서는 X라는 큐를 통해 서비스 A와 C가 연결되고, Y라는 큐를 통해 서비스 B와 D가 마찬가지로 지점 간 연결이 있음을 분명히 알 수 있습니다.
큐와 토픽을 C4 컨테이너로 모델링하면 배포 토폴로지와 독립적으로 생각할 수 있는 방법도 제공됩니다. 개발 시에는 노트북의 리소스를 절약하기 위해 메시지 버스의 단일 인스턴스에서 모든 큐와 토픽을 실행할 수 있습니다. 라이브 배포 토폴로지에서는 성능, 확장성 또는 보안상의 이유로 개별 큐와 토픽이 별도의 메시지 버스, 브로커 또는 클러스터에 배포될 수 있습니다.
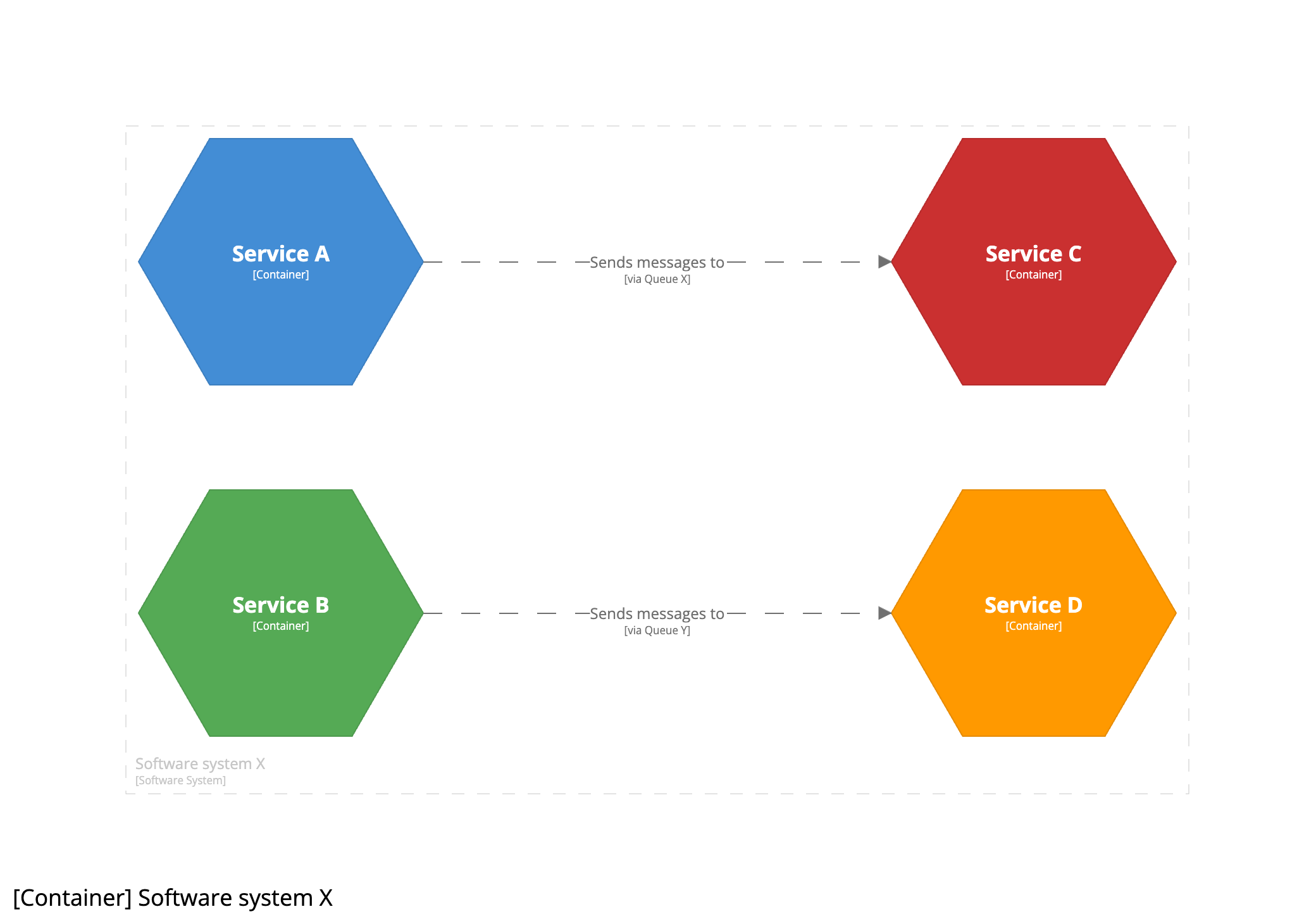
실제로 큐를 통해 지점 간 연결이 있는 경우 큐를 생략하고 대신 큐 이름을 화살표로 이동하여 이 다이어그램을 더욱 단순화할 수 있습니다.
다이어그램이 시각적으로 더 단순해졌지만, 큐가 더 이상 다이어그램에서 명확하게 드러나지 않습니다. C4 모델은 표기법에 독립적이므로 메시지 기반 관계를 강조하기 위해 다른 선 스타일(실선 대 점선) 또는 색상을 추가로 사용할 수 있습니다. 어느 버전의 다이어그램이 다른 버전보다 “더 나은” 것은 아니며, 단지 같은 이야기를 다른 방식으로 전달할 뿐입니다. 모두 장단점이 있습니다.
발행/구독(Pub/Sub)
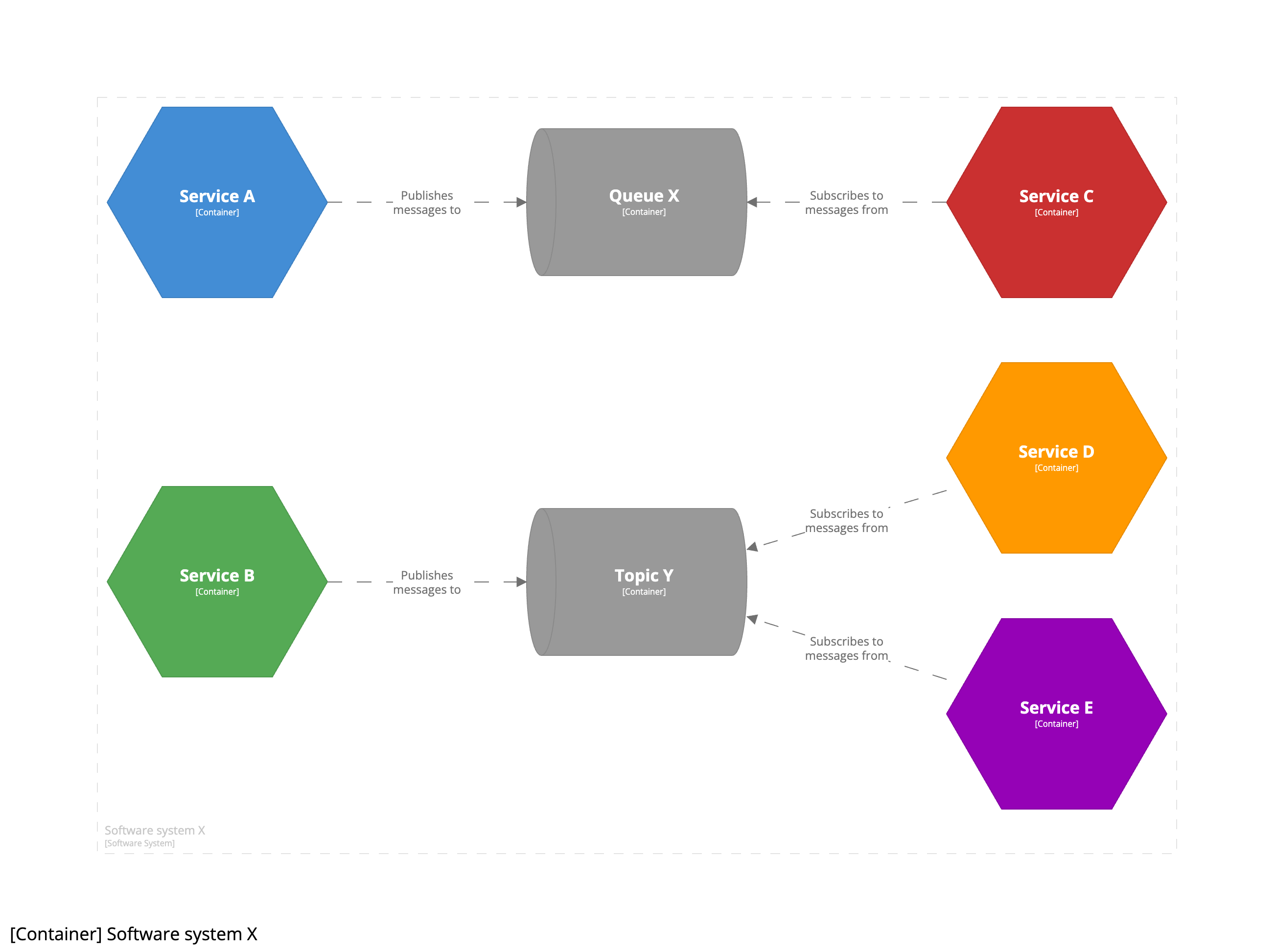
모든 다이어그램에서 메시지가 다이어그램 왼쪽에서 오른쪽으로 흐르며, 화살표에는 “메시지를 보내는 대상”이라는 레이블이 붙어 있음을 볼 수 있습니다. 이 방법은 특히 지점 간 및 큐 기반 아키텍처에 적합하지만, 화살표 방향을 변경하여 더 많은 발행/구독 또는 토픽 기반 아키텍처를 더 잘 나타낼 수도 있습니다.
이 버전의 다이어그램은 메시지 발행자와 구독자의 역할을 더 잘 보여줍니다. 다시 말하지만, 같은 내용을 다른 방식으로 표현한 것일 뿐입니다.
결론
메시지 기반 아키텍처를 다이어그램화하는 방법에는 여러 가지가 있으며, 다음 중 마지막 두 가지가 “올바른” 방법입니다.
- 오답: 메시지 버스를 C4 컨테이너로 모델링합니다.
- 정답: 큐와 토픽을 C4 컨테이너로 명시적으로 모델링합니다.
- 정답: 관계에 “경유(via)” 표기법을 사용하여 메시지 기반 상호작용을 암시적으로 모델링합니다.
기타 고려 사항
앞선 예에서는 하나의 소프트웨어 시스템이 큐와 토픽을 통해 통신하는 여러 서비스로 구성되어 있다고 가정했습니다. 즉, 다이어그램의 모든 것이 소프트웨어 시스템 경계 “내부”에 있으며 해당 단일 소프트웨어 시스템에 의해 “소유”됩니다.
마이크로서비스 권장 사항을 읽고 각 서비스를 별도의 소프트웨어 시스템으로 모델링하는 경우에는 큐와 토픽을 누가 “소유”하는지도 추가로 고려해야 합니다. 서비스 A(소프트웨어 시스템)가 X(컨테이너)라는 이름의 큐를 통해 서비스 B(역시 소프트웨어 시스템)와 지점 간 관계를 갖는다면 누가 이 컨테이너를 소유할까요? 큐의 메시지 형식과 작동 방식에 대한 정의는 서비스 A가 소유하고 있나요, 아니면 서비스 B가 소유하고 있나요? 아니면 공동으로 소유하거나 완전히 다른 누군가가 전적으로 소유하고 있을 수도 있습니다. 이러한 소유권은 다이어그램에 영향을 미칩니다.